Photogalerie „Die Ästhetik im Chaos“

Ordnung im scheinbaren Chaos und Selbstähnlichkeit waren Konzepte, die der französische Mathematiker Benoit Mandelbrot seit den 1960er Jahren wie geisterhafte Schemen in vielen Systemen erkannte. Ein Gebiet von vielen, die er während seiner Zeit in IBMs Grundlagenforschung beackerte, waren die Fluktuationen im Baumwollpreis.
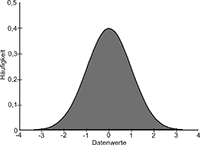Das Standardwerkzeug, um solche Variationen darzustellen, war und ist die Normalverteilungskurve oder auch Glockenkurve (siehe Abbildung), nach dem Mathematiker Johann Carl Friedrich Gauß (1777 bis 1855). Sie zeigt die statistische Verteilung der Datenwerte in Form eines fein abgestuften Balkendiagramms. Entlang seiner horizontalen Achse sind die Datenwerte abgetragen, die Höhe eines Balkens gibt an, wie oft dieser Wert in dem analysierten System vorkommt. Normalerweise verteilen sich die meisten Werte um den Durchschnitt herum, weshalb die Kurve den markanten Hügel in der Mitte aufweist.
Mandelbrots Problem war folgendes: Egal wie er die Baumwollpreise auch analysierte, die Ergebnisse passten nie in die Normalverteilung. Am Ende besorgte er sich alle Baumwollpreisnotierungen bis ins Jahr 1900 zurück und als er diese enorme Datenbasis auf den IBM-Großrechnern analysierte, fiel ihm etwas Bemerkenswertes auf:

Die Datenwerte, die aus der Sicht der Normalverteilung Abweichungen hervorriefen, produzierten Symmetrie, wenn man sie vom Maßstab her betrachtete. Jede einzelne Preisänderung war zufällig und unvorhersagbar. Aber die Sequenz der Änderungen war unabhängig vom Maßstab: Die Kurven für tägliche und monatliche Preisänderungen passten perfekt zueinander, waren deckungsgleich. Noch unglaublicher: Nach Mandelbrots Art analysiert blieb der Grad der Abweichungen über eine historisch sehr bewegte Epoche von 60 Jahren mit zwei Weltkriegen und einer Depression konstant.

In der Folge analysierte Mandelbrot vom elektrischen Rauschen über die Wasserstände großer Flüsse und die Länge von Küstenlinien zahlreiche andere Phänomene und fand in allen Selbstähnlichkeit und Skaleninvarianz. Aber die Formen der klassischen euklidischen Geometrie – Linien, Ebenen, Kreise, Kugeln, Dreiecke und Kegel – waren nicht geeignet, die Komplexität dieser Gestalten zu erfassen. Mandelbrot sagte gern:

Wolken sind keine Kugeln, Berge keine Kegel, Küstenlinien keine Kreise. Die Rinde ist nicht glatt – und auch der Blitz bahnt sich seinen Weg nicht gerade.

Euklids 2000 Jahre alte Arbeit, die sich in jeder praktischen Hinsicht als mächtige Abstraktion der Wirklichkeit erwiesen hatte, entging das wahre Wesen der genarbten, krummen, gebrochenen, verwickelten und ineinander greifenden Dinge, die wir jeden Tag um uns herum beobachten können. Ja sie ist nicht einmal in der Lage, die exakte Länge einer solchen Gestalt anzugeben.
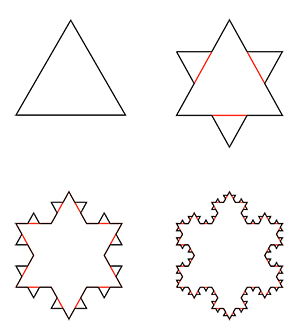Ein Beispiel ist die Koch-Kurve, erstmals 1904 von dem schwedischen Mathematiker Helge von Koch vorgestellt. So, wie die meisten selbstähnlichen Formen, entsteht auch die Koch-Kurve durch Iteration (lat. Iterare: wiederholen). Dieser mathematische Begriff meint eine Methode, sich der Lösung eines Rechenproblems schrittweise aber zielgerichtet anzunähern. Sie besteht in der wiederholten Anwendung desselben Rechenverfahrens. In der Regel iteriert man mittels Rückkopplung. Die Ergebnisse eines Rechenschrittes werden also zum Ausgangswerte des jeweils nächsten Schrittes. Dieser Ersetzungsvorgang wird immer wieder, theoretisch sogar unendlich oft ausgeführt. Um eine Koch-Kurve zu konstruieren, nehmen Sie ein gleichseitiges Dreieck und ergänzen das mittlere Drittel jeder Seite durch ein weiteres gleichseitiges Dreieck. Dies Hinzufügen setzen Sie beliebig oft fort (siehe Abbildung).
Diese so einfach zu erstellende Kurve weist schon nach wenigen Durchgängen einen Komplexitätsgrad auf, der in der euklidischen Geometrie selten anzutreffen ist. Will man aber die Länge der Kurve ermitteln, kommt man in Schwierigkeiten. Setzen wir den Initiator mit der Länge 1 an, so beträgt die Kurvenlänge im ersten Schritt 1,333, im zweiten 1,778, im dritten 2,370, im vierten 3,160, im fünften 4,214 und nach unendlich vielen Rechenschritten wäre die Kurve unendlich lang.
Ein weiteres Beispiel sind die Längen von Küstenlinien. Die Karte eines solchen Verlaufs zeigt viele kleine Buchten. Messen wir aber die Länge anhand der Abbildung, so lassen wir zwangsläufig jene Buchten aus, die zu klein sind, um abgedruckt zu werden. Aber auch beim Abschreiten der Küste verpassen wir viele mikroskopisch kleine Buchten zwischen den Sandkörnern. – Egal wie sehr wir die Küstenlinie auch vergrößern, es wird bis hinunter auf die atomare Ebene immer noch mehr Buchten geben.
Koch-Kurve und Küstenlinie bringen beide ein interessantes Paradox ans Licht. Denn mit jedem zusätzlichen Dreieck bzw. jeder weiteren Vergrößerungsstufe verlängert sich die jeweilige Linie zwar, die von ihr umfasste Fläche bleibt aber geringer als die eines Zirkelschlages um die Ausgangsgestalt. Beide Linien sind also von potenziell unendlicher Länge, umgeben aber eine begrenzte Fläche.
Weitere Phänomene, auf die die genannten Attribute zutreffen, sind die Formen von Bergen und Flüssen, Verästelungen von Pflanzen, Blutgefäßen und Lungenbläschen, die Verteilung von Sternhaufen in Galaxien und die Pfade der Wärmebewegung von Teilchen in Flüssigkeiten und Gasen (Brownsche Bewegung). Auch der Herzschlag des Menschen, seine Gehirnströme und Atemrhythmus folgen fraktalen Rhytmen. Werden sie zu regelmäßig, kann das zu Herzversagen durch Stauung, Atemnot oder epileptischen Anfällen führen. Im normalen Leben schwanken all diese Rhythmen also beständig im Grenzbereich zwischen Chaos und Ordnung hin und her. Des Weiteren finden sich solche Strukturen auch in quantitativen Beschreibungen menschlichen Schaffens und Handelns, etwa in der Musik, der Malerei und der Architektur sowie in Börsenkursen.