Photogalerie „Die Ästhetik im Chaos“

Den nächsten wichtigen Schritt in der Chaosforschung machte der Biologe Robert May zu Beginn der 1970er Jahre. Er befasste sich mit der Vorhersage biologischer Populationen – ein Feld, in dem die Ergebnisse ebenfalls sehr stark von den Ausgangsbedingungen abhängen. Müsste man nicht limitierende Faktoren, wie Fressfeinde und begrenzte Nahrungsressourcen berücksichtigen, wäre die Sache eine einfache Multiplikation und das Ergebnis eines Jahres wäre der Ausgangswert des nächsten. Die einfachste Gleichung, die die begrenzenden Faktoren mit einbezieht, ist:

Population des nächsten Jahres =
Geburtenrate * Aktuelle Population * (1 – Aktuelle Population)

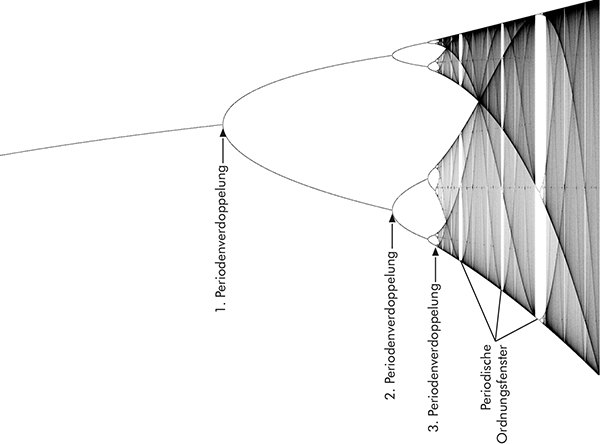
Robert May spielte mit unterschiedlichen Geburtenraten, um zu sehen, was mit den Ergebnissen passiert. Er erkannte, daß sich die Populationsgröße bei geringer Geburtenrate auf einen stabilen Wert einpendelte und mit steigender Geburtenrate ebenfalls zunahm. Dies Verhalten galt bis zu einem bestimmten Punkt. Passierte ihn die Geburtenrate, so spaltete sich der Graph und das Ergebnis sprang zwischen zwei Werten A und B hin und her. Für ein Jahr wäre es A, für das nächste B und dieser Zyklus wiederholte sich für immer. Rechnete er mit einer noch höheren Geburtenrate, so ergaben sich vier zyklisch wechselnde Ergebnisse und diese Verdoppelungen (Bifurkationen) kamen mit weiter steigendem Ausgangswert immer schneller und schneller. Ab einer bestimmten Größe wurde es dann allerdings unmöglich, ein Ergebnis zu bestimmen. Dies war die Grenze, ab der Chaos eintrat. Aber das war nicht das Interessanteste. Interessant war vielmehr, daß das Diagramm in diesem chaotischen Bereich weiße Streifen zeigt, in denen die Gleichung die Verdoppelungen wiederholte, bevor sie wieder ins Chaos zurück fällt. Der Graph zeigt also tief drinnen exakte verkleinerte Kopien seiner selbst. So ein Verhalten wird Selbstähnlichkeit genannt und sie ist ein wichtiger Aspekt des Chaos. May erkannte zwar die geometrische Besonderheit seines Diagramms, hielt sie aus seiner biologischen Perspektive aber für eine mathematische Absonderlichkeit. Es blieb mit Mitchell Feigenbaum einem Physiker überlassen, die wahre Bedeutung der Periodenverdoppelungen zu erkennen.
Feigenbaum untersuchte seit 1974 am Los Alamos National Laboratory Turbulenzen in Flüssigkeiten. Im Sommer des Jahres 1975 hörte er einen Vortrag über quadratische Differenzialgleichungen, ähnlich denen die Lorenz verwendet hatte, und auf einer abstrakten Ebene war ihm klar, daß sie jene geheimnisvolle Grenze zwischen dem sanften Dahinfließen und der Turbulenz seiner Flüssigkeiten beschrieben. Also machte er sich mit dem Universalwerkzeug seiner Wissenschaftsgeneration, dem ersten programmierbaren Taschenrechner HP-65, daran, die exakten Werte der Periodenverdoppelungen zu berechnen. Am Ende war es wohl die Langsamkeit seines Rechenknechts, welche ihm zwischen dem Notieren des einen Ergebnisses und dem Warten auf das nächste die zündende Eingebung bescherte: Er erkannte, daß die Zahlen genauso konvergierten, wie eine Reihe Begrenzungspfähle an einer geraden Straße. Wenn man weiß, wie groß zwei beliebige dieser reflektierenden Gesellen sind, kennt man auch die Größen aller anderen. Feigenbaum errechnete als Verhältnis der Konvergenz den Wert 4,669, die 1. Feigenbaum-Konstante.
Bezogen auf Mays Bifurkations-Diagramm hatte er damit den Maßstab gefunden, auf dem sich seine Selbstähnlichkeit abspielt: Verkleinert man das Diagramm 4,669 mal, so sieht es aus wie die nächstfolgende Periodenverdoppelung.
Bis ins folgende Jahr untersuchte Feigenbaum andere einfachere und kompliziertere Gleichungen, die alle Systeme beschrieben, welche aus einem Zustand der Ordnung über eine Serie Periodenverdoppelungen ins Chaos übergehen. Zu seiner großen Überraschung produzierten sie alle denselben Verhältniswert von 4,669 zwischen den Bifurkationen. Das war nicht weniger als revolutionär, denn es bedeutete, daß sich eine ganze Klasse mathematischer Funktionen in derselben vorhersagbaren Weise verhielt. Fließende Gewässer, schwingende Pendel und elektronische Oszillatoren, sie alle folgen auf ihrem Weg von der Vorhersagbarkeit zur Unvorhersagbarkeit einem universellen Naturgesetz und bilden deshalb Formen heraus, die sich jeweils auf einer tiefen Ebene alle gleichen.